Stats
Data Visualisation
Visualisation: Histogram
- Relative Frequency Histogram
- Shows the location of the centre of the data
- Shows the spread of the data
Skewness
Data skewed to the right (positively skewed) have a longer right tail
Dot plots
A graph of quantitative data where each data value is plotted as a dot above a horizontal scale of values.
Dots representing equal values are stacked.
Stem plots(Stem-and-Leaf plot)
Represents quantitative data by separating each value into two parts: the stem and the leaf
Time-Series Graph
A graph of time-series data
Pie Chart
Frequency Polygon
Pictograph
Representing data using images
Hints
- Be careful w Nonzero Vertical Axis
Descriptive Stat
Measure of center: a value at the center/middle of a data set
Mean(Average)
Median: The value that cuts the data exactly in half
Mode: The value in the data set that occurs most frequently
Midrange:$\frac{Max+Min}{2}$, not resistant
Measures of Variation
Describe how spread out the point in a data set are.
Range
$Range = Max-Min$
Variance
A measure of how much the data values deviate from the mean.
Population consisting of N values
$\sigma ^2=\frac{(x_1-\mu)^2+\cdots+(x_n-\mu)^2}{N}=\frac{1}{N}\sum\limits_{i=1}^N(x_i-\mu)^2$
Sample consisting of n values
$s^2=\frac{(x_1-\overline{\mu})^2+\cdots+(x_n-\overline{\mu})^2}{n - 1}=\frac{1}{n-1}\sum\limits_{i=1}^n(x_i-\overline{x})^2$
never negative, zero only when all of the data values are exactly the same
Not resistant cuz its sensitive to extreme values
why use (n-1) to compute $s^2$
It makes $s^2$ an unbiased estimator of $\sigma^2$
Standard Deviation
Square root of the variance
Population standard deviation
$\sigma=\sqrt{\sigma^2}$
Sample standard deviation
$s=\sqrt{s^2}$
Standard Scores(z-scores)
The number of standard deviations that x lies above the mean
population
$z=\frac{x-\mu}{\sigma}$
sample
$z=\frac{x-\overline{x}}{s}$
if $x < \overline{x} \text{ or x} < \mu$ then $z < 0$
Percentiles
kth Percentile
A value $P_k$ such that k% of the values in the data set lie below it
Median: 50th percentile
first quartile $Q_1$: 25th percentile
third quartile $Q_3$: 75 percentile
IQR
$IQR=Q_3-Q_1$
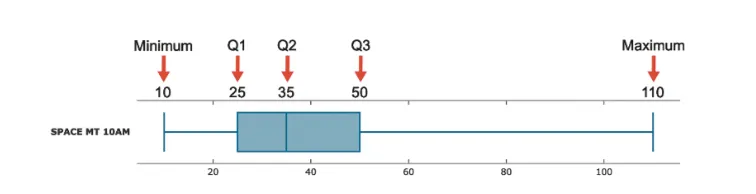
Five-Number Summary
A concise summary of the data using five numbers:
Minimum, $Q_1$, Median, $Q_3$, Maximum
Boxplots
- A line extending from the minimum value to the maximum value
- A box with lines drawn at $Q_1$, the median and $Q_3$
- A method for visulizing the five-number summary of a data set
Modifies Boxplots
Modify the original boxplot to show extreme observations or outliers
Find the quartiles $Q_1,Q_2,Q_3$
Compute $IQR=Q_3-Q_1$
In a modifies boxplot, a data value is considered an outlier
if it is greater than $Q_3+1.5 \cdot IQR$ or it is less than $Q_1-1.5 \cdot IQR$
A special symbol is used to identify outliers
The solid horizontal line extends only as far as the minimum data value that is not an outlier and the maximum data value that is not an outlier
Probability
Law of Large Numbers
The relative frequency probability of an event tends to approach the actual probability.
Subjective Probability
Estimate the probability of an event by using knowledge of the relevant circumstances
Mutually Exclusive Events
A and B never occur at the same time
Repeatedly sample items from a population
- Sampling with replacement
- Each time observe the item and put it back in the population
- Sampling without replacement
- Each time observe it and remove it from the population
Bayes Theorem
$P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\frac{P(B|A)P(A)}{P(B|A)P(A)+P(B|\overline{A})P(\overline{A})}$
Permutations: $P(n,r)=\frac{n!}{(n-r)!}$
Combinations:$C(n,r)=\frac{n!}{(n-r)!r!}$
Discrete Probability Distributions
Random Variable
A number with each outcome in the sample space S in a proabbility experiment.
$$X: S \rightarrow \mathbb{R}, i.e, \ \text{A function mapping outcomes in S to real numbers}$$
Discrete Random Variables
A random variable is discrete if it can take a finite or countably infinite number of different values
Continuous Random Variables
A random variable is continuous if it can take on an infinite number of different values that cannot be listed
Discrete Probability Distribution
Probability Mass Function
$p(x)=P(X=x)$
$\sum\limits_xp(x)=1$
Mean/Variabnce/Standard Deviation
Mean of X(Expected value of X)
$\mu=\sum\limits_xx\cdot p(x)$
Variance of X
$\sigma_x^2=\sum\limits_x[x^2\cdot p(x)]-\mu^2=\sum\limits_x(x-\mu )^2\cdot p(x)$
Standard Deviation
$\sigma_x=\sqrt{\sigma_x^2}$
Binomial Distribution
Binomial Random Variable
X = number of successes in the n trials
Probability Mass Function
A binomial experiment consisting of n trials with proabbility of success p
If X is the binomial random variable for thie experiment
$X$ ~ $Bin(n,p)$
$p(x)=P(X=x)=_nC_x p^x(1-p)^{n-x}$
Mean/Variance/Standard Deviation
$\mu_x=np$
$\sigma_x^2=np(1-p)$
$\sigma_x=\sqrt{np(1-p)}$
Poisson Distribution
$P(x)=\frac{\mu^x\cdot e^{-\mu}}{x!}$ $(x=0,1,2\cdots)$
$x$ ~ $Poiss(\mu)$
Assumption: Occurrences are:
- Random
- Independent of one another
- Uniformly distributed over the interval being used
Mean
$\mu_x=\mu$
Variance
$\sigma_x^2=\mu$
Standard Deviation
$\sigma_x=\sqrt{\mu}$
Probability Density Function
- $f(x)\geq 0$ for all x
- The total area under the graph of f equals 1
Standard Normal Distribution
$f(z)=\frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}$
$-\infty < z < \infty$
Normal Distribution
A continous random variable X has a normal distribution with parameters $-\infty < \mu < \infty$ and $\sigma^2 >0$ if it has a probability density function of the form
$f(x)=\frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}},-\infty < x < \infty$
A standard normal distribution: $\mu = 0$, $\sigma=1$, $Z$~ $N(0,1)$
Mean/Variance/Standard Deviation
$X$~ $N(\mu,\sigma^2)$
$\mu_x=\mu$, $\sigma_x^2=\sigma^2$, $\sigma_x=\sigma$
Standardise
Z-Score
$Z=\frac{x-\mu}{\sigma}$
$Z$~ $N(0,1)$
$z_{0.05}=1.645$, 95% confidence level
Sampling Distribution
$\overline{X}$ ~ $N(\mu, \frac{\sigma^2}{n})$
if Sample is normal, sample mean is also normal with mean $\mu$ and standard deviation $\frac{\sigma}{\sqrt{n}}$
n increases, the standard deviation $\frac{\sigma}{\sqrt{N}}$ of $\overline{X}$ gets smaller
Larger samples yield less variability in sample mean
Central Limit Theorem
$X_1,X_2,\cdots,X_n$ : a random sample from a distribution with mean $\mu$ and standard deviation $\sigma$
If n is sufficiently large, $\overline{X}$ has approximately a $N(\mu,\frac{\sigma^2}{n})$ distribution
$X_1 + X_2 + \cdots + X_n = n \overline{X}$ also approximately normal
Point and Interval Estimation
Point Estimate
A point estimate $\hat{\theta}$ of a parameter $\theta$ is a single number that can be regarded as a sensible value for $\theta$
Unbiased Estimator
A point estimator $\hat{\theta}$ of a parameter $\theta$ is unbiased if $E(\hat{\theta})=\theta$
MVUE: Minimum variance unbiased estimator
Theorem: Let $X_1, X_2, \cdots, X_n$ be a random sample from a normal distribution with Mean $\mu$ and variance $\sigma^2$. Then the estimator $\hat{\mu}=\overline{X}$ is the MVUE for $\mu$
Interval Estimation
Estimate a range of possible values for our parameter
Since $X_1, X_2, \cdots, X_n$ are drawn from a normal distribution with mean $\mu$ and variance $\sigma^2$, $\overline{X}$~ $N(\mu,\frac{\sigma}{n})$
Standardize $\overline{X}$ like $Z=\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}$
We have Z ~ N(0,1)
Common Critical Values
Common Confidence Level Critical Value
0.90 1.645
0.95 1.96
0.99 2.575
Normal Confidence Interval for $\mu$($\sigma$ known)
Let $X_1, X_2, \cdots, X_n$ be a random sample from a normal distribution with unknown mean $\mu$ and known standard deviation $\sigma$
For Any $0 \leq \alpha \leq 1$, a $100(1-\alpha)%$ confidence interval for $\mu$ is:
$\overline{X}-z_{\frac{\alpha}{2}}\cdot \frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\frac{\alpha}{2}}\cdot \frac{\sigma}{\sqrt{n}}$
$P(\overline{X}-z_{\frac{\alpha}{2}}\cdot \frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\frac{\alpha}{2}}\cdot \frac{\sigma}{\sqrt{n}})=1-\alpha$
Normal Confidence Interval for $\mu$($\sigma$ unknown)
Let $X_1, X_2, \cdots, X_n$ be a random sample from a normal distribution with unknown mean $\mu$ and known standard deviation $\sigma$
Use sample standard deviation S to estimate the population stadard deviation $\sigma$
$T=\frac{\overline{X}-\mu}{S/ \sqrt{n}}$
T has t distribution with (n-1) degrees of freedom(df)
t distribution
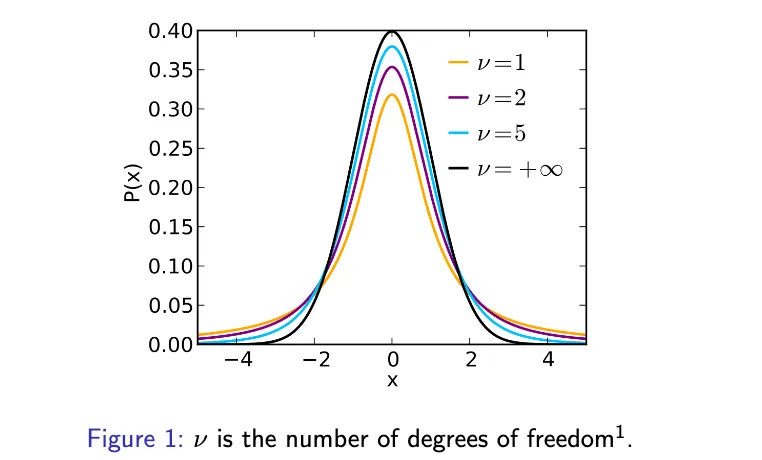
One single parameter: degrees of freedom v (in our case, v = n - 1)
The distribution is symmetric
Mean is zero.
As df v gets really large, t distribution looks more like a standard normal distribution.
If T has such a distribution,
$t_{\alpha, n - 1}$ is the value such that $P(T>t_{\alpha, n-1})=\alpha$
$P(-t_{\frac{\alpha}{2},n-1}<T<t_{\frac{\alpha}{2},n-1}) = 1 - \alpha$
$P(-t_{\frac{\alpha}{2},n-1}<\frac{\overline{X}-\mu}{S/ \sqrt{n}}<t_{\frac{\alpha}{2},n-1}) = 1 - \alpha$
$P(\overline{X}-t_{\frac{\alpha}{2},n-1}\cdot \frac{S}{\sqrt{n}} < \mu < \overline{X}+t_{\frac{\alpha}{2},n-1}\cdot \frac{S}{\sqrt{n}})=1-\alpha$
$(0 \leq \alpha \leq 1, 100(1-\alpha)$% $\text{confidence interval for }\mu)$
Large Sample Confidence Interval for $\mu$
Let $X_1, X_2, \cdots, X_n$ be a random sample from a normal distribution with unknown mean $\mu$ and known standard deviation $\sigma$(not necessarily a normal distribution)
For any $0 \leq \alpha \leq 1$, an approximate $100(1-\alpha)$ % confidence interval for $\mu$ is as follows
$\overline{X}-z_{\frac{\alpha}{2}}\cdot \frac{S}{\sqrt{n}} < \mu < \overline{X}+z_{\frac{\alpha}{2}}\cdot \frac{S}{\sqrt{n}}$
Control the interval width
suppose normally distributed with $\sigma$
$\overline{X}-z_{\frac{\alpha}{2}}\cdot \frac{\sigma}{\sqrt{n}} < \mu < \overline{X}+z_{\frac{\alpha}{2}}\cdot \frac{\sigma}{\sqrt{n}}$
width of this confidence interval is $w=2z_{\frac{\alpha}{2} }\cdot \frac{\sigma}{\sqrt{n}}$
$n=(\frac{2z_{\frac{\alpha}{2}}\sigma}{w})^2$
Confidence Interval for p
A binomial experiment with n trials and an unknown probability of success p. Let X be the number of successes in the n trials.
natural point estimator for p is $\hat{p} =\frac{X}{N}$ i.e, the proportion of success in the n trials
if both $np \geq 10$ and $n(1-p) \geq 10$,then $\hat{p}$ approximately normally distributed by the Central Limit Theorem
$\hat{p} \approx N(p, \frac{p(1-p)}{n})$
Standardising $\hat{p}$
$Z=\frac{\hat{p}-p}{\sqrt{p(1-p)/n}} \approx N(0,1)$
$P(-z_{\frac{\alpha}{2}}< \frac{\hat{p}-p}{\sqrt{p(1-p)/n}} < z_{\frac{\alpha}{2}}) \approx 1-\alpha$
$0 \leq \alpha \leq 1$, appr $100(1-\alpha)$ % CI for p
$\frac{\hat{p}+z_{\alpha / 2}^2 / 2 n}{1+z_{\alpha / 2}^2 / n} \pm z_{\alpha / 2} \frac{\sqrt{\hat{p}(1-\hat{p}) / n+z_{\alpha / 2}^2 / 4 n^2}}{1+z_{\alpha / 2}^2 / n}$
Hypothesis Testing
| Decision | H₀ is True | H₀ is False |
|---|---|---|
| Fail to Reject H₀ | Correct Decision | Type II Error |
| Reject H₀ | Type I Error | Correct Decision |
$\alpha=P$(Type I Error)
$\beta=P$(Type || Error)
$\beta$ depends on the true value of the parameter we’re testing
Controlling $\beta$ can get complicated, so we can control $\alpha$
A hypothesis test with a probability $\alpha$ of making a Type I error is known as a level $\alpha$ test
Tests of $H_0:\mu=\mu_0$
Consider a sample $X_1, X_2, \cdots, X_n$ from a normal distribution with mean $\mu$ and standard deviation $\sigma$. Suppose $\sigma$ is known
Two-tailed test of $H_0:\mu=\mu_0$
A leval $\alpha$ test of $H_0$: $\mu=\mu_0$ vs $H_1:\mu \neq \mu_0$ is as follows
Reject $H_0$ if $Z < -z_{\alpha/2}$ or $Z > z_{\alpha/2}$
The test statistic:
$Z=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}$
| H1 | Reject $H_0$ if |
|---|---|
| $\mu \neq \mu_0$ | $z < -z_{\alpha/2}$ or $z > z_{\alpha/2}$ |
| $\mu < \mu_0$ | $z < -z_{\alpha}$ |
| $\mu > \mu_0$ | $z > z_{\alpha}$ |
Inferences from Two Samples
Comparing Independent Populations
$H_0:\mu1-\mu2 = 0,H_1: \mu1-\mu2 \neq 0$
$\overline{X}-\overline{Y}$ is an unbiased estimator of $\mu1-\mu2$
Since populations are normal $\overline{X}-\overline{Y}$ has a normal distribution
Assuming that $H_0$ is true, then $\mu1-\mu2=0$
$\overline{X}-\overline{Y}$ ~ $N(0,\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n})$
Standardize
$Z=\frac{\overline{X}-\overline{Y}}{\sqrt{\sigma_1^2/m+\sigma_2^2/n}}$~N(0,1)
Reject $H_0$ if z < $-z_{\alpha/2}$ or $z > z_{\alpha/2}$
Generalise to different $H_1$
| H1 | Reject $H_0$ if |
|---|---|
| $\mu_1 - \mu_2 \neq 0$ | $z$ < $-z_{\alpha/2}$ or $z > z_{\alpha/2}$ |
| $\mu_1-\mu_2 < 0$ | $z < -z_{\alpha}$ |
| $\mu_1-\mu_2 > 0$ | $z > z_{\alpha}$ |
Confidence Interval for $\mu_1-\mu_2$
construct a $100(1-\alpha)$% CI for $\mu_1-\mu_2$
$\overline{X}-\overline{Y}$~ $N(\mu_1-\mu_2, \frac{\sigma^2}{m}+\frac{\sigma^2}{n})$
Standardize
$Z=\frac{\overline{X}-\overline{Y}-(\mu_1-\mu_2)}{\sqrt{\sigma_1^2/m+\sigma_2^2/n}}$~N(0,1)
$P(-z_{\alpha/2}<\frac{\overline{X}-\overline{Y}-(\mu_1-\mu_2)}{\sqrt{\sigma_1^2/m+\sigma_2^2/n}}<z_{\alpha/2})=1-\alpha$
CI: $\overline{X}-\overline{Y} \pm z_{\alpha/2} \cdot \sqrt{\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}}$
Two-Sample t Test
Under $H_0$, test statistic
$T = \frac{\overline{X}-\overline{Y}}{\sqrt{S_1^2/m+S_2^2/n}} \approx t_{\nu}$
Degree of freedom $\nu$, round down to the nearest whole number
$\nu =\frac{(s_1^2/m+s_2^2/n)^2}{\frac{(s_1^2/m)^2}{m-1}+\frac{(s_2^2/n)^2}{n-1}}$
| H1 | Reject $H_0$ if |
|---|---|
| $\mu_1 - \mu_2 \neq 0$ | $t < -t_{\alpha/2,\nu}$ or $t > t_{\alpha/2,\nu}$ |
| $\mu_1-\mu_2 < 0$ | $t < -t_{\alpha,\nu}$ |
| $μ1−μ2>0$ | $t > t_{\alpha,\nu}$ |
Pooled t Test
Under the assumption $\sigma_1=\sigma_2$
Pooled estimator of $\sigma^2$
$S_p^2 = \frac{m - 1}{m + n - 2} S_1^2 + \frac{n - 1}{m + n - 2} S_2^2$
$\nu = m + n - 2$
CI
$\bar{X}-\bar{Y} \pm t_{\alpha/2,\nu} \cdot\sqrt{\frac{S_1^2}{m}+\frac{S_2^2}{n}}$
Paired t Test
data of pairs: $(X_1,Y_1), (X_2, Y_2),\cdots,(X_n,Y_n)$
Differences: $D_1=Y_1-X_1, D_2=Y_2-X_2, \cdots, D_n=Y_n-X_n$
test $H_0:\mu_D=0$ against $H_1:\mu_D \neq 0, H_1:\mu_D>0,H_1:\mu_D<0$
Construct level $\alpha$ tests
test statistic $T=\frac{\bar{D}}{S_D/ \sqrt{n}}$~ $t_{n-1}$
| H1 | Reject $H_0$ if |
|---|---|
| $\mu_D \neq 0$ | $t < -t_{\alpha/2,n-1}$ or $t > t_{\alpha/2,n-1}$ |
| $\mu_D< 0$ | $t < -t_{\alpha,n-1}$ |
| $\mu_D>0$ | $t > t_{\alpha,n-1}$ |
Confidence Interval for $\mu_D$
$P(-t_{\alpha/2,n-1}<\frac{\bar{D}}{S_D/ \sqrt{n}}<t_{\alpha/2,n-1})=1-\alpha$
CI: $\bar{D} \pm t_{\alpha/2,n-1} \cdot \frac{S_D}{\sqrt{n}}$
Comparing Population Proportions
Proportion of successes for the two population: p1, p2
Test the hypotheses
$H_0:p1-p2 = 0$ against $H_1: p1-p2 \neq 0,H_1:p1-p2>0, H_1:p1-p2<0$
x: the number of success in the sample from the first population
y: the number of success in the sample from the second population
then x and y each have binomial distribution
Use sample proportions $\hat{p_1}=\frac{x}{m}$ and $\hat{p_2}=\frac{y}{n}$ to develop a test statistic
suppose $H_0$ is true, then p1=p2=p
If $np \geq 10, n(1-p) \geq 10$
then the following test statistic has an approximate normal distribution
(Application of the Central Limit Theorem)
$z = \frac{\hat{p_1}-\hat{p_2}}{\sqrt{p(1-p)(\frac{1}{m}+\frac{1}{n}})}$~N(0,1)
Since we are assuming p1=p2=p(i.e, $H_0$ is true), we can use data from both samples to estimate the common p
The natural estimator of p is
$\hat{p}=\frac{x+y}{m+n}=\frac{m}{m+n} \cdot \hat{p_1} + \frac{n}{m+n} \cdot \hat{p_2}$
substitute $\hat{p}$ for $p$
$z = \frac{\hat{p_1}-\hat{p_2}}{\sqrt{\hat{p}(1-\hat{p})(\frac{1}{m}+\frac{1}{n})}}$ ~N(0, 1)
Must Assume: $m\hat{p_1} \geq 10, m(1-\hat{p_1}) \geq 10, n\hat{p_2} \geq 10, n(1-\hat{p_2}) \geq 10$
| H1 | Reject $H_0$ if |
|---|---|
| $p_1 - p_2 \neq 0$ | $z$ < $-z_{\alpha/2}$ or $z > z_{\alpha/2}$ |
| $p_1-p_2 < 0$ | $z < -z_{\alpha}$ |
| $p_1-p_2 > 0$ | $z > z_{\alpha}$ |
Correlation
Covariance
positive relationship
$S_{xy}=\frac{1}{n} \sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})>0$
Analogously, negative relationship betweeen $x_i$ and $y_i$, covariance $S_{xy}$ Negative
Pearson Correlation coefficient
$r=\frac{S_{xy}}{\sqrt{S_{xx}\cdot S_{yy}}}=\frac{\sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum\limits_{i=1}^n(x_i-\bar{x})^2\cdot \sum\limits_{i=1}^n(y_i-\bar{y})^2}}$
r close to 1 indicate a strong positive linear relationship;
r close to -1 indicate a strong negative linear relationship
r = 0 indicates the lack of a linear relationship between x and y
Tests of $H_0: \rho=0$
$H_1: \rho \neq 0, H_1: \rho < 0, H_1: \rho > 0$
$T = \frac{R\sqrt{n-2}}{\sqrt{1-R^2}}$~ $t_{n-2}$
| H1 | Reject $H_0$ if |
|---|---|
| $\rho \neq 0$ | $t < -t_{\alpha/2,n-2}$ or $t > t_{\alpha/2,n-2}$ |
| $\rho< 0$ | $t < -t_{\alpha,n-2}$ |
| $\rho>0$ | $t > t_{\alpha,n-2}$ |
Linear Regression
Simple Linear Regression
There are parameters $\beta_0, \beta_1, \sigma^2$ such that for any fixed value of the independent variable x, the dependent variable is related to x through the model equation
$Y - \beta_0+\beta_1x+\epsilon$
Assume the error quantity $\epsilon$~ $N(0,\sigma^2)$
Least Squares Estimates
Find values of $b_0$ and $b_1$ that minimize $\sum_{i=1}^n(y_i-(b_0+b_1x_i))^2$
$b_0-\hat{\beta_0}$ and $b_1-\hat{\beta_1}$ that minimize this quantity are the least squares estimates of $\beta_0$ and $\beta_1$
In the case of simple linear regression
$\hat{\beta_1}=r \cdot \frac{S_y}{S_x}$, $\hat{\beta_0}=\bar{y}-\hat{\beta_1}\bar{x}$
$\hat{\beta_1}$ has the same sign as the correlation coefficient r
$\hat{y}=\hat{\beta_0}+\hat{\beta_1}x$
Assessing Model Fit
residuals
$y_i-\hat{y_i}$
Prediction Interval
A range of values used to estimate a variable
A range of plausible values for the corresponding value of y:
$\hat{y} \pm t_{\alpha/2,n-2}s_e \sqrt{1+\frac{1}{n}+\frac{n(x-\bar{x})^2}{n(\sum_{i=1}^n x_i^2)-(\sum_{i=1}^n x_i)^2}}$
$s_e=\sqrt{\frac{\sum_{i=1}^n(y_i-\bar{y})}{n-2}}$
Relies on the assumption that the errors $\epsilon$ are normally distributed with mean 0 and a shared standard deviation $\sigma$
Total Variation
$\sum_{i=1}^n(y_i-\bar{y})^2$
Decompose:
$\sum_{i=1}^n(y_i-\bar{y})^2=\sum_{i=1}^n(\hat{y_i}-\bar{y})^2+\sum_{i=1}^n(y_i-\hat{y})^2$
total variation = explained variation + unexplained variation
Coefficient of determination
$R^2=\frac{\text{explained variation}}{\text{total variation}}$
$0 \leq R^2 \leq 1$ Ideally $R^2$ close to 1
In the case of simple linear regression $R^2=r^2$
Multiple Linear Regression
$Y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_k x_k + \epsilon$
Error term $\epsilon$ ~ $N(0, \sigma^2)$
Find a good model
- Use domain knowledge to determine which likely useful variables
- Plot the residuals, which should look like random noise
- Create a normal Q-Q plot of the residuals to access. (Straight line)
- Examine $R_{adj}^2$
- Conduct a hypothesis test of $H_0:\beta_1 = \beta_2 = \cdots =\beta_k = 0$
Adjusted Coefficient of Determination
n: sample size k: number of independent variables
$R_{adj}^2 = 1 - \frac{n-1}{n-(k+1)}(1-R^2)$
Formal Test of Model Utility
Assuming the residuals appear to be drawn from a normal distribution
Hypotheses:
$H_0: \beta_1 = \beta_2=\cdots=\beta_k = 0$
$H_1: \text{at least one } \beta_i \neq 0$
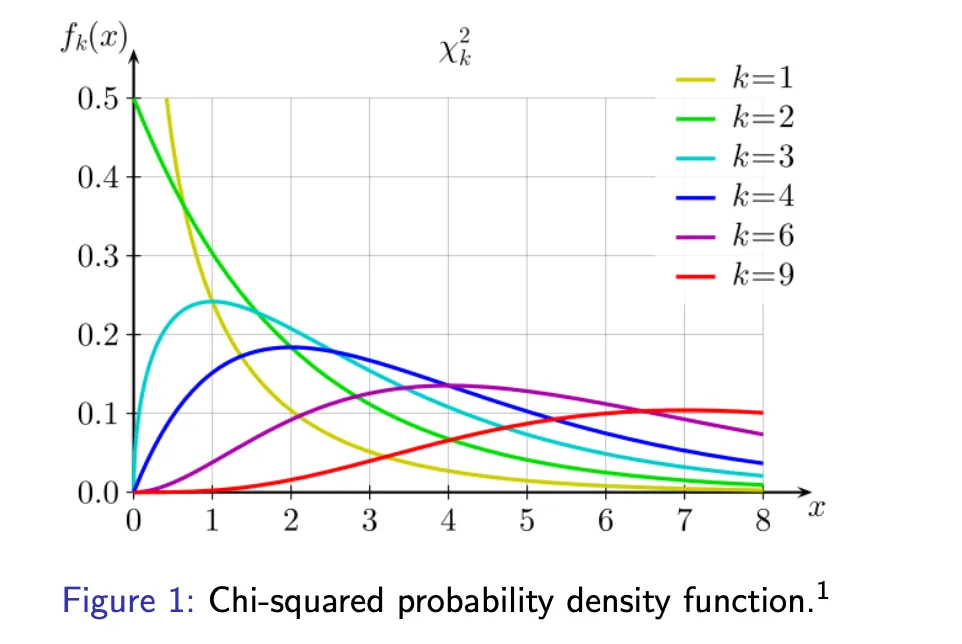
F-distribution
Dummy variables
numerical encoding of a qualitative variable
Goodness-of-Fit
Pearson’s Chi-Squared Test
Test at level $\alpha$
$H_0: p_1 = p_{10}, p_2=p_{20}, \cdots, p_k = p_{k0}$
$H_1: \text{at least one } p_i \text{ not equal to } p_{i0}$
Check $np_{0i} \geq 5$
Test statistic: $\chi ^2 = \sum\limits_{i = 1}^k \frac{(n_i - np_{i0})^2}{np_{i0}}$
Reject $H_0$ if $\chi^2 > \chi_{\alpha, k-1}^2$
Caesar Ciphers
To encrypt text
shift the alphabet the the left by a fixed amount
Contingency Tables
Test of Homogeneity
Test at level $\alpha$
$H_0: p_{1j}=p_{2j}=\cdots = p_{Ij}$
$H_1: H_0 \text{ is not true}$
Check that $\hat{e_{ij}} \geq 5$ for each i and j
test statistic
$\chi^2 = \sum\limits_{i=1}^I \sum\limits_{j=1}^J \frac{(n_{ij} - \hat{e_{ij}})^2}{\hat{e_{ij}}}$
Reject $H_0$ at level $\alpha$ if $\chi ^2 > \chi_{\alpha, (I-1)(J-1)}^2$
Test of Independence
Test at level $\alpha$
$H_0: p_{ij} = p_i \cdot p_j$
$H_1: H_0 \text{ is false}$
Check that $\hat{e_{ij}} \geq 5$ for each i and j
test statistic
$\chi^2 = \sum\limits_{i=1}^I \sum\limits_{j=1}^J \frac{(n_{ij} - \hat{e_{ij}})^2}{\hat{e_{ij}}}$
Reject $H_0$ at level $\alpha$ if $\chi ^2 > \chi_{\alpha, (I-1)(J-1)}^2$
